사다리꼴 넓이 구하는 공식, 예시
사다리꼴은 초등 고학년부터 중학교 수학 과정까지 반복적으로 등장하는 대표적인 평면도형입니다. 겉보기에는 단순해 보이지만, 평행선의 성질과 삼각형 넓이 공식이 복합적으로 적용되는 구조이기 때문에 개념을 정확히 이해하지 못하면 계산 과정에서 실수가 잦습니다. 특히 “왜 이런 공식이 되는가?”라는 원리를 이해하지 못하면 문제 유형이 조금만 변형되어도 접근이 어려워집니다. 따라서 단순 암기가 아니라 도형의 구조적 해석, 넓이 공식의 유도 과정, 실제 수치 예시 적용까지 단계적으로 정리하는 것이 중요합니다. 본 글에서는 사다리꼴의 정의부터 시작해 넓이 공식의 의미, 다양한 예시 계산, 응용 문제 접근법까지 체계적으로 설명하겠습니다.
사다리꼴의 정의와 기본 구조
사다리꼴은 한 쌍의 대변이 서로 평행한 사각형을 의미합니다. 여기서 평행한 두 변을 밑변이라 하고, 서로 평행하지 않은 두 변을 옆변이라 합니다. 밑변은 위쪽과 아래쪽에 각각 존재하며, 일반적으로 아래쪽을 아랫변, 위쪽을 윗변이라고 구분합니다. 넓이를 구할 때 핵심이 되는 요소는 다음 세 가지입니다.

사다리꼴 넓이 계산에 필요한 기본 요소는 다음과 같습니다.
- 윗변의 길이
- 아랫변의 길이
- 높이
여기서 높이는 두 밑변 사이의 수직 거리입니다. 옆변의 길이는 넓이 계산에 직접적으로 사용되지 않으며, 반드시 ‘수직 거리’라는 점을 명확히 인지해야 합니다.
사다리꼴 넓이 구하는 공식
사다리꼴의 넓이는 다음 공식으로 계산합니다.
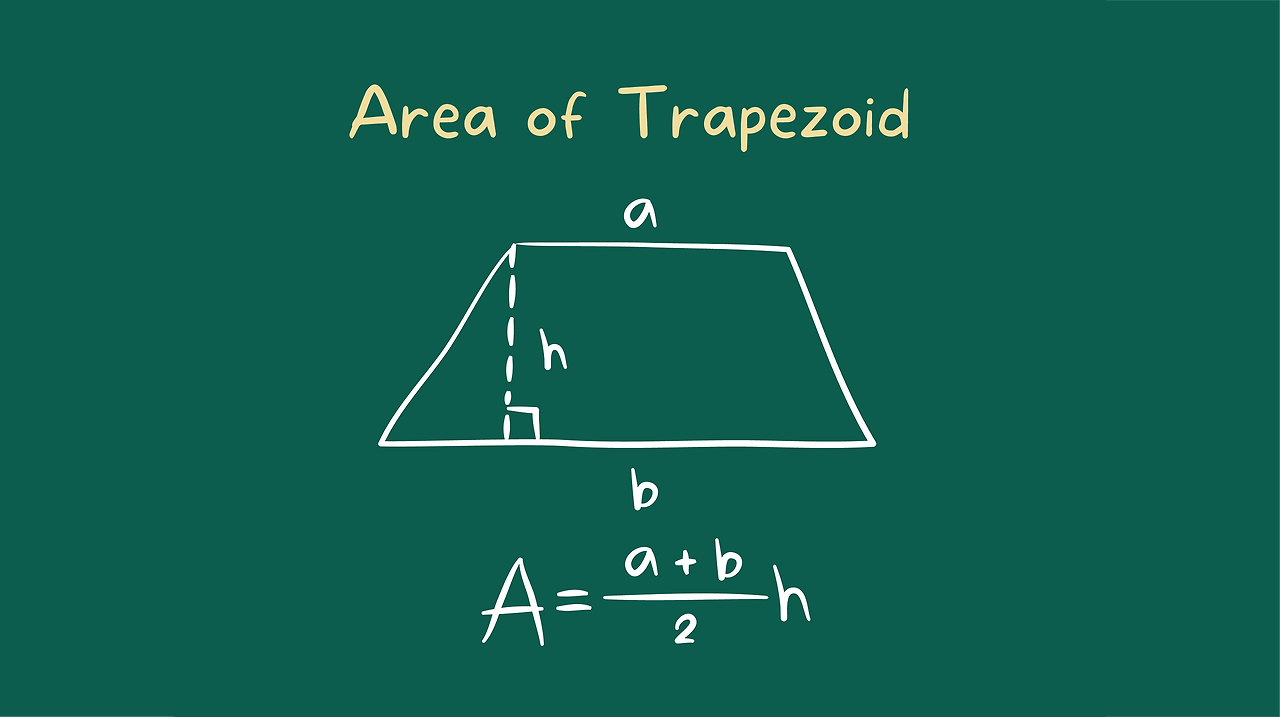
$$ 사다리꼴\ 넓이 = \frac{(윗변 + 아랫변) \times 높이}{2} $$
이 공식을 간단히 정리하면 다음과 같습니다.
- 두 밑변의 길이를 더한다
- 그 합에 높이를 곱한다
- 마지막으로 2로 나눈다
이 공식이 성립하는 이유는 사다리꼴을 동일한 두 개를 이어 붙이면 평행사변형이 되기 때문입니다. 동일한 사다리꼴을 좌우로 뒤집어 붙이면 밑변의 길이는 윗변과 아랫변의 합이 되고, 높이는 그대로 유지됩니다. 평행사변형의 넓이는 밑변 × 높이이므로, 사다리꼴 한 개의 넓이는 그 절반이 됩니다. 따라서 2로 나누는 과정이 포함되는 것입니다.
공식 유도 과정의 이해
사다리꼴의 넓이 공식을 단순 암기하지 않고 이해하기 위해서는 삼각형과 평행사변형 개념을 함께 떠올리는 것이 좋습니다. 사다리꼴을 대각선으로 나누면 두 개의 삼각형이 됩니다. 각 삼각형의 넓이를 더하면 전체 넓이가 되며, 이를 정리하면 결국 위 공식과 동일한 형태로 귀결됩니다.
또 다른 방식으로는 평균 개념을 활용하는 방법이 있습니다. 윗변과 아랫변의 평균 길이에 높이를 곱한 것과 동일하다는 점이 핵심입니다. 즉 다음과 같이 표현할 수 있습니다.
$$ 넓이 = (두\ 밑변의\ 평균) \times 높이 $$
이는 수학적으로도 직관적인 해석이 가능하며, 계산 실수를 줄이는 데 도움이 됩니다.
사다리꼴 넓이 계산 예시 1
구체적인 수치를 통해 계산 과정을 살펴보겠습니다.
예시 조건은 다음과 같습니다.
- 윗변: 6cm
- 아랫변: 10cm
- 높이: 5cm
계산 과정은 다음과 같습니다.
- 두 밑변을 더합니다. → 6 + 10 = 16
- 높이를 곱합니다. → 16 × 5 = 80
- 2로 나눕니다. → 80 ÷ 2 = 40
따라서 넓이는 40㎠입니다.
사다리꼴 넓이 계산 예시 2
이번에는 조금 더 복잡한 수치를 적용해 보겠습니다.
조건은 다음과 같습니다.
- 윗변: 8m
- 아랫변: 14m
- 높이: 7m
계산은 다음과 같습니다.
- 8 + 14 = 22
- 22 × 7 = 154
- 154 ÷ 2 = 77
따라서 넓이는 77㎡입니다. 단위가 바뀌면 반드시 최종 단위도 함께 표기해야 합니다.
높이가 주어지지 않은 경우의 접근
일부 문제에서는 높이가 직접적으로 주어지지 않고, 옆변의 길이나 각도가 주어지는 경우가 있습니다. 이때는 직각삼각형의 성질을 활용하여 높이를 먼저 구해야 합니다.
접근 절차는 다음과 같습니다.
- 옆변과 밑변 차이를 활용하여 직각삼각형 구성
- 피타고라스 정리 적용
- 높이 산출 후 공식 대입
이 과정은 중학교 과정 이상에서 자주 등장하는 유형이며, 단순 공식 암기보다 기하적 해석 능력이 중요합니다.
특수한 사다리꼴의 넓이
사다리꼴에는 여러 변형 유형이 존재합니다. 대표적인 유형은 다음과 같습니다.
- 등변사다리꼴
- 직각사다리꼴
등변사다리꼴은 옆변의 길이가 같으며 대칭 구조를 가집니다. 직각사다리꼴은 한 옆변이 밑변과 수직을 이룹니다. 그러나 넓이 공식은 변하지 않습니다. 핵심은 항상 두 밑변과 높이입니다.
계산 시 자주 발생하는 실수
사다리꼴 문제에서 자주 나타나는 오류 유형은 다음과 같습니다.
- 옆변을 높이로 착각
- 두 밑변을 곱한 뒤 2로 나누는 오류
- 평균 개념을 오해하여 (윗변 + 아랫변) ÷ 2만 계산하고 높이를 곱하지 않는 실수
- 단위 변환 누락
이러한 실수는 개념 이해 부족에서 비롯됩니다. 계산 전 반드시 ‘수직 높이’인지 확인하는 습관이 필요합니다.
응용 문제 접근 전략
시험이나 평가에서는 다음과 같은 응용 형태가 출제됩니다.
- 사다리꼴을 포함한 복합 도형 넓이 계산
- 사다리꼴 넓이를 이용해 미지수 구하기
- 도형 변형 후 넓이 비교
이 경우 기본 공식을 정확히 이해하고 있어야 하며, 도형을 분해하거나 재구성하는 능력이 중요합니다. 특히 넓이 보존 원리를 활용하면 계산을 단순화할 수 있습니다.
결론
사다리꼴 넓이 공식은 단순히 외워야 할 공식이 아니라, 평행사변형과 삼각형의 성질을 응용한 결과입니다. 두 밑변의 합에 높이를 곱하고 2로 나누는 구조는 ‘평균 × 높이’라는 개념으로도 이해할 수 있습니다. 기본 구조를 이해하면 어떠한 수치가 주어져도 일관된 방식으로 접근할 수 있으며, 응용 문제에서도 당황하지 않게 됩니다. 도형 문제는 원리 이해가 곧 문제 해결 능력입니다. 공식의 의미를 정확히 이해하고 다양한 예시를 통해 반복 연습한다면 계산 실수를 최소화할 수 있습니다.



