구의 면적 구하는 공식

구의 면적 구하는 공식

기하학에서 구는 가장 기본적이면서도 동시에 가장 많은 응용을 갖는 입체 도형 중 하나입니다. 중학교와 고등학교 과정에서는 원의 넓이와 원기둥, 원뿔의 부피를 배우고, 그 연장선에서 구의 겉넓이와 부피를 다루게 됩니다. 특히 구의 면적, 정확히는 구의 겉넓이는 단순 암기 대상처럼 보이지만, 그 공식이 왜 그렇게 되는지를 이해하면 미적분, 물리, 공학으로 자연스럽게 확장됩니다. 이 글에서는 구의 면적 구하는 공식을 단순히 제시하는 데 그치지 않고, 구의 면적 구하는 공식이 어떻게 유도되는지, 그리고 실제 계산에 활용할 수 있도록 파이썬 프로그램 예제까지 체계적으로 설명드립니다.

구의 면적 구하는 공식

구의 면적은 구의 바깥을 감싸는 전체 표면의 넓이를 의미하며, 일반적으로 ‘겉넓이’라는 표현을 사용합니다.

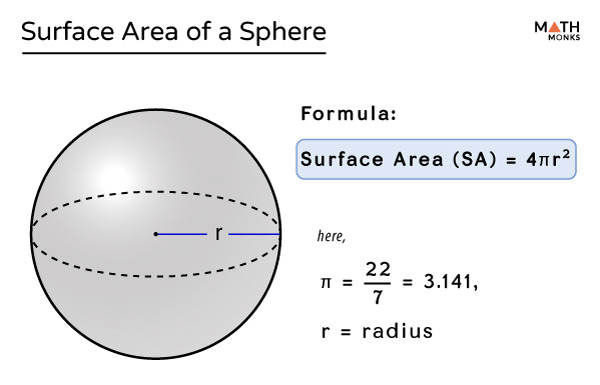
반지름을 r이라고 할 때 구의 면적 공식은 다음과 같습니다.

$$S = 4\pi r^2$$

이 공식은 매우 간단해 보이지만, 원의 넓이 공식 $$\pi r^2$$과 비교해 보면 흥미로운 구조를 갖습니다. 구의 면적은 같은 반지름을 가진 원 넓이의 정확히 4배에 해당합니다. 이 관계는 단순한 우연이 아니라 기하학적, 해석학적 구조에서 자연스럽게 도출된 결과입니다.

구의 면적 공식에서 사용되는 각 요소를 정리하면 다음과 같습니다.

• r: 구의 반지름
• π: 원주율로 약 3.14159
• 4: 구 전체 표면이 반지름 r을 기준으로 네 개의 동일한 면적 구조를 갖는다는 기하학적 결과

이 공식은 단위 체계와 무관하게 동일하게 적용됩니다. 반지름이 cm라면 면적 단위는 cm², m라면 m²가 됩니다. 중요한 점은 반지름의 제곱에 비례하므로, 반지름이 두 배가 되면 구의 면적은 네 배가 된다는 점입니다. 이는 물리학에서 열 방출, 중력, 전자기학 등 다양한 분야에서 매우 중요한 의미를 가집니다.

구의 면적 구하는 공식 유도하는 방법

구의 면적 공식은 단순 암기가 아니라, 여러 방법으로 유도할 수 있습니다. 대표적인 접근은 미적분학적 사고를 이용하는 방식입니다. 구를 무한히 얇은 띠들의 집합으로 생각하면, 각 띠의 넓이를 적분해 전체 면적을 구할 수 있습니다.

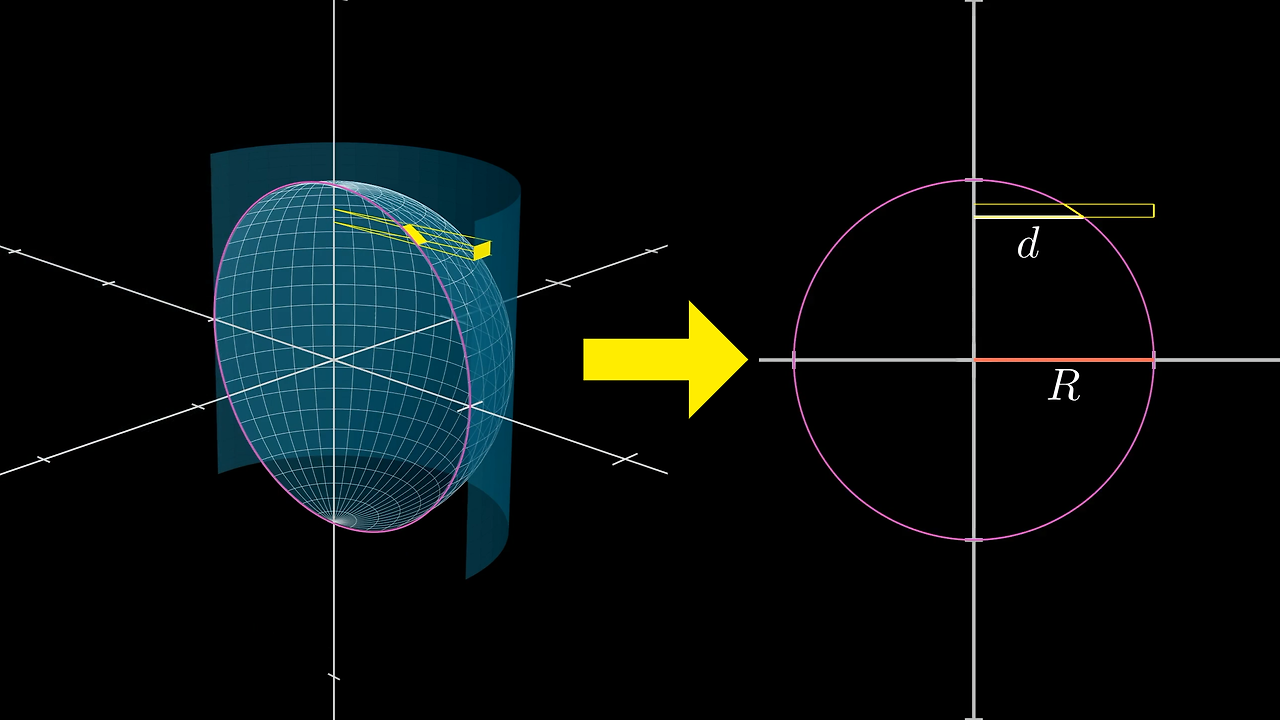
가장 직관적인 유도 방법은 구를 위도 방향의 얇은 원띠들의 집합으로 보는 것입니다. 반지름 r인 구에서 중심을 기준으로 높이 x에 위치한 단면은 반지름이 $$\sqrt{r^2 - x^2}$$인 원이 됩니다. 이 원의 둘레는 $$2\pi\sqrt{r^2 - x^2}$$이며, 두께 dx를 곱하면 아주 얇은 띠의 면적 요소 dS는 다음과 같이 표현됩니다.
$$dS = 2\pi\sqrt{r^2 - x^2},dx$$

이제 구의 전체 면적은 x가 -r에서 r까지 변할 때 이 미소 면적을 모두 더한 값이 됩니다. 즉,
$$S = \int_{-r}^{r} 2\pi\sqrt{r^2 - x^2},dx$$

이 적분은 반원 넓이와 관련된 표준 적분으로 계산할 수 있으며, 결과는 다음과 같이 정리됩니다.
$$\int_{-r}^{r} \sqrt{r^2 - x^2},dx = \frac{\pi r^2}{2}$$

이를 앞의 식에 대입하면,
$$S = 2\pi \times \frac{\pi r^2}{2} \times 2 = 4\pi r^2$$

이로써 구의 면적 공식이 엄밀하게 유도됩니다. 이 과정에서 중요한 점은 구의 표면을 평면적으로 펼칠 수 없더라도, 미적분을 이용하면 면적을 정확히 계산할 수 있다는 사실입니다. 또한 이 결과는 아르키메데스가 이미 고대에 원기둥과 구의 관계를 통해 직관적으로 밝혀낸 사실이기도 합니다. 같은 반지름과 높이를 가진 원기둥의 옆넓이와 구의 겉넓이가 같다는 점은 수학사적으로도 매우 유명한 성질입니다.

구의 면적 구하는 파이선 프로그램 소스

구의 면적 공식은 프로그래밍에서도 매우 자주 사용됩니다. 과학 계산, 시뮬레이션, 그래픽 처리, 물리 엔진 등 다양한 분야에서 구의 표면적 계산이 필요합니다. 파이썬에서는 수학 라이브러리를 이용해 간단하게 구현할 수 있습니다.

아래는 반지름을 입력받아 구의 면적을 계산하는 가장 기본적인 예제입니다.

import math

def sphere_surface_area(r):
    return 4 * math.pi * r ** 2

radius = float(input("구의 반지름을 입력하세요: "))
area = sphere_surface_area(radius)
print("구의 면적:", area)

이 코드에서 핵심 요소를 정리하면 다음과 같습니다.

• math.pi를 사용하여 원주율을 정확하게 처리
• r ** 2를 통해 반지름의 제곱 계산
• 함수 형태로 정의하여 재사용 가능하도록 구성

조금 더 확장하면 여러 개의 반지름에 대해 한 번에 계산하거나, 단위 변환까지 포함할 수 있습니다. 예를 들어 반지름 목록을 입력받아 각각의 구 면적을 계산하는 방식도 가능합니다.

import math

radii = [1, 2.5, 5, 10]

for r in radii:
    area = 4 * math.pi * r ** 2
    print(f"반지름 {r}인 구의 면적: {area}")

이처럼 구의 면적 공식은 단순한 수학 문제를 넘어, 실제 계산과 자동화에 매우 적합한 구조를 갖고 있습니다. 특히 지수적 증가 특성을 갖기 때문에 수치적 안정성과 단위 관리가 중요하며, 이를 코드로 구현할 때 명확히 인식하는 것이 필요합니다.

결론

구의 면적 구하는 공식 $$S = 4\pi r^2$$는 단순하지만 깊은 의미를 지닌 수학적 결과입니다. 이 공식은 원의 넓이에서 출발해 미적분학으로 확장되며, 고대 수학부터 현대 과학기술까지 폭넓게 활용되고 있습니다. 공식의 유도 과정을 이해하면 단순 암기를 넘어, 왜 반지름의 제곱에 비례하는지, 왜 계수가 4π인지 명확히 설명할 수 있습니다. 또한 파이썬과 같은 프로그래밍 언어로 구현하면 추상적인 수식이 실제 계산 도구로 전환되며, 수학적 사고와 실무적 활용을 동시에 강화할 수 있습니다. 구의 면적 공식은 기하학 학습의 중요한 이정표이자, 수학적 사고를 한 단계 확장시키는 핵심 개념이라 할 수 있습니다.